

We also provide extensive NCERT solutions, sample papers, NEET, JEE Mains, BITSAT previous year papers, which makes us a one-stop solution for all resources. Physics Wallah is India's top online ed-tech platform that provides affordable and comprehensive learning experience to students of classes 6 to 12 and those preparing for JEE and NEET exams.
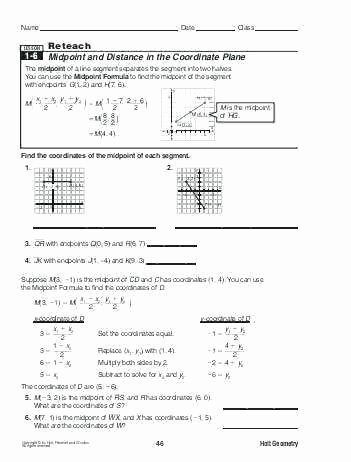
You would repeat the Y-values process to find the midpoint's Y-coordinate. If one X-value is at 2 and the other X-value is at 8, to find the X-value halfway between them, you add 2+8 and divide by 2 = 5. The Midpoint Formula does the same thing.
So with the part of the line, use this formula to calculate the point that divides the part of the line defined by two points.Īns. The midpoint formula is used when a person is required to find a straight center position between two defined points.
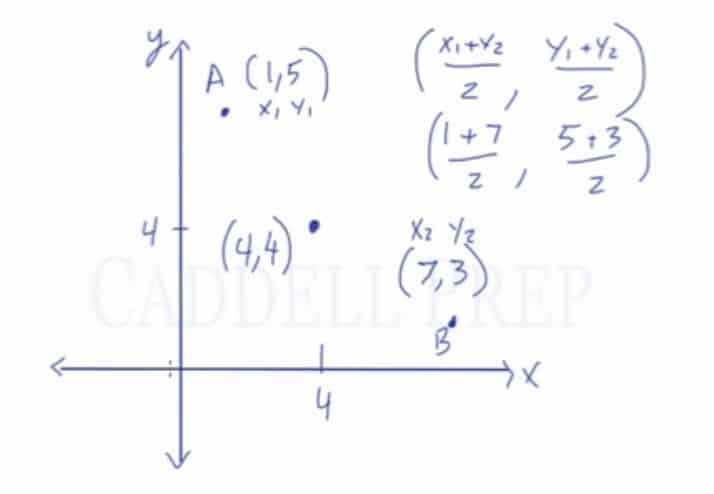
Why is the midpoint formula essential?Īns. To find the midpoint of any range, add the two numbers together and divide by 2. What is the formula for finding the midpoint?Īns. He was thrilled with his invention, which he called a method, for it used algebra to combine arithmetic and geometry and unified all the mathematics known up to that time. Rene Descartes, born in 1596, invented the idea o geometrically representing ordered pairs of numbers. The section formula builds on it and is a more powerful tool it locates the point dividing the line segment in any desired ratio.Īns. The midpoint of a line segment is the point that divides a line segment into two halves. What is the difference between mid point formula and section formula?Īns. Thus, the required ratio is 1/2 : 1 or 1 : 2. But it is a point on x-axis on which y-coordinate of every point is zero. Then the coordinates of the point of division are. In what ratio does the X-axis divide the line segment joining the points (2, –3) and (5, 6)?Īns. Let the required ratio be k : 1. Thus C divides AB externally in the ratio 5 : 8. īut we are given that the coordinates of the points C are (-1, -1). In which ratio does the point (–1, –1) divide the line segment joining the pints (4, 4) and (7, 7)?Īns. Suppose the point C(-1, -1) divides the line joining the points A(4, 4) and B(7, 7) in the ratio k : 1. Find the coordinates of the point which divides the line segment joining the points (6, 3) and (–4, 5) in the ratio 3 : 2 (i) internally (ii) externally. If λ is +ve then it is internal division and if λ is –ve then it is external division. Evaluate the value of λ i.e., the ratio.Ĥ. To find the ratio in which the line divides the line joining the two points.ģ. Note: The line joining the points is divided by the x-axis in the ratio and by x axis in the ratio Hence the coordinates of the midpoint of AB are. So by the section formula, the coordinates of M are Proof: Let M be the midpoint of the line segment joining the points The coordinates of the midpoint M of a line segment AB with end points A(x 1, y 1) and B(x 2, y 2) are. In the same way, we use the midpoint formula for coordinate geometry to find the average number (i.e., point) of two coordinates. Thus, you get the ratio of these two numbers. Sometimes you will need to find half of two specific numbers. A Midpoint formula is used to determine the center point of a straight line.


 0 kommentar(er)
0 kommentar(er)
